搜索结果: 1-15 共查到“理学 PDE”相关记录29条 . 查询时间(0.026 秒)
Academy of Mathematics and Systems Science, CAS Colloquia & Seminars:"Inverse problems for elliptic PDE" (8)
椭圆偏微分方程 反问题 Calderón问题
2023/11/29
Academy of Mathematics and Systems Science, CAS Colloquia & Seminars:"Inverse problems for elliptic PDE" (7)
椭圆偏微分方程 反问题 Calderón问题
2023/11/29

吉林大学举办 “基于机器学习的PDE数值计算与应用”线上研讨会(图)
吉林大学 机器学习 PDE数值计算 线上研讨会
2020/7/21
跨越时空,“云”上相聚。2020年7月13日,由国家自然科学基金数学天元基金和吉林大学共同资助,国家天元数学东北中心和吉林大学联合承办的“基于机器学习的PDE数值计算与应用”研讨会在线举行。本次研讨会由基金委数理学部主任江松院士召集,来自普林斯顿大学、布朗大学、哥伦比亚大学、洛桑联邦理工学院,北京大学、浙江大学、复旦大学、上海交通大学、吉林大学等国内外百余所高校的800余位专家学者和学生齐聚云端,...
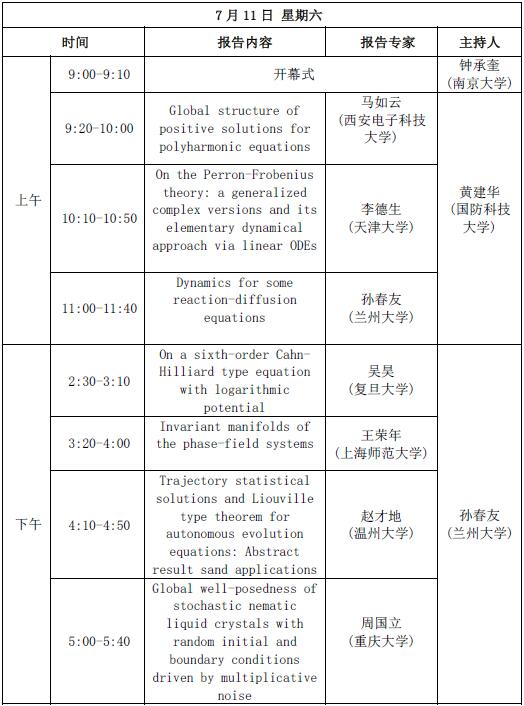
2020年无穷维动力系统与PDE学术研讨会(图)
2020年 无穷维动力系统 PDE 学术研讨会
2020/8/19
无穷维动力系统&PDEs是基础数学中非常重要的研究领域,在材料力学、流体力学和大气科学等领域具有广泛的应用。为了进一步加强无穷维动力系统&PDEs研究领域学者之间的交流与合作,定于2020年7月11-12日举办“2020年云端无穷维动力系统&PDEs学术研讨会”。本次会议涵盖无穷维动力系统中的吸引子理论和静态统计性质、不变流形、中心流形及偏微分方程分歧理论、均质化理论和正则性理论等。
基于周期理论和COMSOL PDE的排桩减振特性研究
周期排桩 COMSOL PDE 衰减域 环境减振
2018/11/29
基于周期理论和COMSOL PDE有限元法,研究了排桩的衰减域(attenuation zone,简称AZ),讨论了相关参数对衰减域的影响;针对实测环境振动设计了具体的排桩结构,并对该排桩的减振特性在频域和时域内分别进行了数值模拟。研究结果表明:周期理论可以用于揭示排桩的动力特性,为排桩结构在环境减振中的应用提供新思路;基于控制方程建模的COMSOL PDE有限元法,不仅能够用于周期结构的衰减域计...

第一届全国PDE博士生论坛顺利召开(图)
第一届 全国 PDE博士生 论偏微分方程
2018/11/15
2018年11月10日-11日,第一届全国PDE博士生论坛在复旦大学举行。中国科学院院士洪家兴、陈恕行、江松和来自北京大学、清华大学、中国人民大学、浙江大学、中国科学技术大学、上海交通大学、南京大学、中山大学、厦门大学、四川大学、武汉大学、中国科学院数学与系统科学研究院、德国莱比锡大学、香港科技大学等国内外高校和研究院所的近百位专家学者和研究生参加论坛。复旦大学研究生院常务副院长吴宏翔老师,复旦大...
2017年流体和等离子体中的偏微分方程模型和非线性研讨会(PDE Models and Nonlinear Waves in Fluids and Plasmas Workshop)
2017年 流体和等离子体中的偏微分方程模型和非线性 研讨会
2017/11/24
Incompressible and compressible fluids pose many important mathematical physics problems, which are crucial to understand the practical problems from gas dynamics, weather forecast, ocean waves and th...
三亚国际数学论坛:PDE Models and Nonlinear Waves in Fluids and Plasmas
三亚国际数学论坛 PDE Models and Nonlinear Waves in Fluids and Plasmas
2017/7/3
Incompressible and compressible fluids pose many important mathematical physics problems, which are crucial to understand the practical problems from gas dynamics, weather forecast, ocean waves and th...
Nonlinear Stochastic Perturbations of Dynamical Systems and Quasi-linear Parabolic PDE’s with a Small Parameter
Quasi linear parabolic equations parameters quasi linear initial boundary value
2015/9/28
In this paper we describe the asymptotic behavior, in the exponential time scale, of solutions to quasi-linear parabolic equations with a small parameter at the second order term and the long time beh...
Averaging principle for quasi-linear parabolic PDE’s and related diffusion processes
Quasi linear disturbance two dimensional flow parabola and small parameter
2015/9/28
Quasi-linear perturbations of a two-dimensional flow with a first integral and the corresponding parabolic PDE’s with a small parameter at the second order derivatives are considered in th...
On a fully non-linear elliptic PDE in conformal geometry
Fully nonlinear PDE generalized Yamabe problem
2014/4/3
We give an expository survey on the subject of the Yamabe-type problem and applications. With a recent technique in hand, we also present a simplified proof of the result by Chang-Gursky-Yang on...
Designing Optical Fibers: Fitting the Derivatives of a Nonlinear Pde-Eigenvalue Problem
Symmetric Indefinite Eigenvalue Gradient Optical Fiber Design
2013/1/30
When trying to fit data to functions of the eigensystem of a pde-eigenvalue problem, such as Maxwell’s equation, numerical differentiation is ineffective and analytic gradients must be supplied. In ou...
Consistency Analysis of Finite Difference Approximations to PDE Systems
systems of partial differential equations involution Thomas decomposition finite difference approximations consistency
2011/9/16
Abstract: In the given paper we consider finite difference approximations to systems of polynomially-nonlinear partial differential equations whose coefficients are rational functions over rationals i...
On the Quasi-Linear Elliptic PDE $-\nabla\cdot(\nabla{u}/\sqrt{1-|\nabla{u}|^2}) = 4π\sum_k a_k δ_{s_k}$ in Physics and Geometry
Lorentz manifolds maximal foliations lightcone singularities
2011/9/15
Abstract: It is shown that for each finite number of Dirac measures supported at points $s_n$ in three-dimensional Euclidean space, with given amplitudes $a_n$, there exists a unique real-valued Lipsc...
Algebra properties for Sobolev spaces- Applications to semilinear PDE's on manifolds
Sobolev spaces Riemannian manifold algebra rule paraproducts heat semigroup
2011/9/15
Abstract: In this work, we aim to prove algebra properties for generalized Sobolev spaces $W^{s,p} \cap L^\infty$ on a Riemannian manifold, where $W^{s,p}$ is of Bessel-type $W^{s,p}:=(1+L)^{-s/m}(L^p...


